Shaders in sketches — Distance
Hola,
It’s been a while since the last time, but it’s shader time!
If you haven’t read my previous issue, read it here. And the very first one was published on my blog.
After the last GLSL function explored in this 'Shaders in sketches' series — length(), I thought continuing with distance() would make sense.
Distance function
Let's travel through the distance() function, which calculates the distance between two points:
distance(p0, p1) The links in the references below give us a description of this GLSL function:
distance returns the distance between the two points p0 and p1.
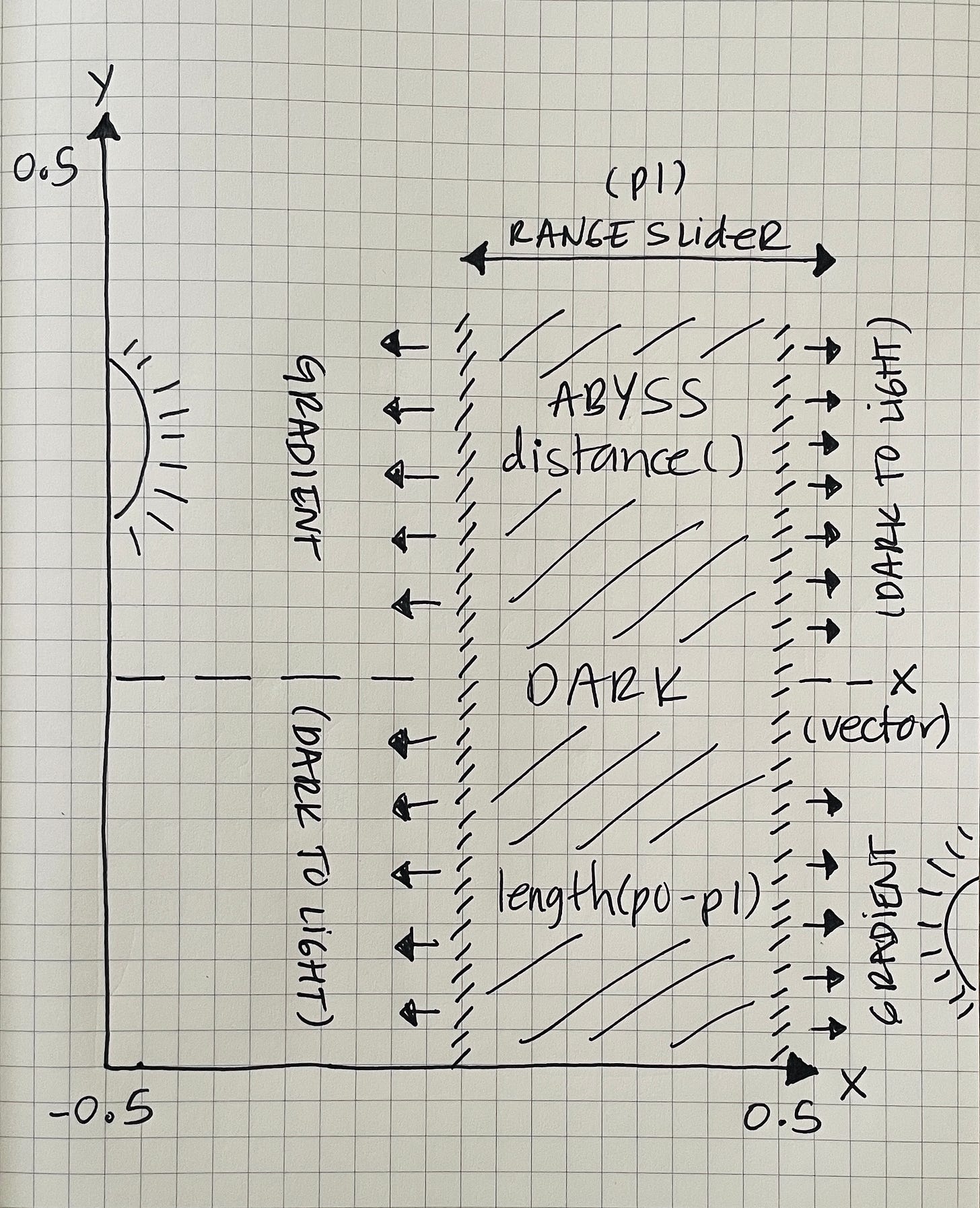
But what does that mean? Like with length(), my aha moment arrived once I visualized the function as an abyss in the middle of a space (the distance between two points) — a luminosity gradient going from dark (abyss) to light (space) but with an additional element in the mix — a range slider to move the abyss on a specific coordinate space.
If we center our coordinate system to have a 0 value in the middle of our screen, and take the x-coordinate as the first point (p0) to use in the distance() function including a floating-point number of 0.25 as the second point (p1), we can imagine a flat vertical abyss of darkness in the right half of the screen. The abyss wouldn’t be a solid block of color but more of a murkiness eroding in light, appearing visually as two linear gradients mirrored together. The imaginary range slider (p1) allows us to move the abyss along its x-coordinate (p0), thus if we’d like to have our abyss centered, we’d assign a 0.0 to p1.
To visualize instead a flat horizontal abyss of murkiness at the top of the screen, we’d assume our first point (p0) in the distance() function is the y-coordinate, and the second point (p1), aka imaginary range slider, a value of 0.25.
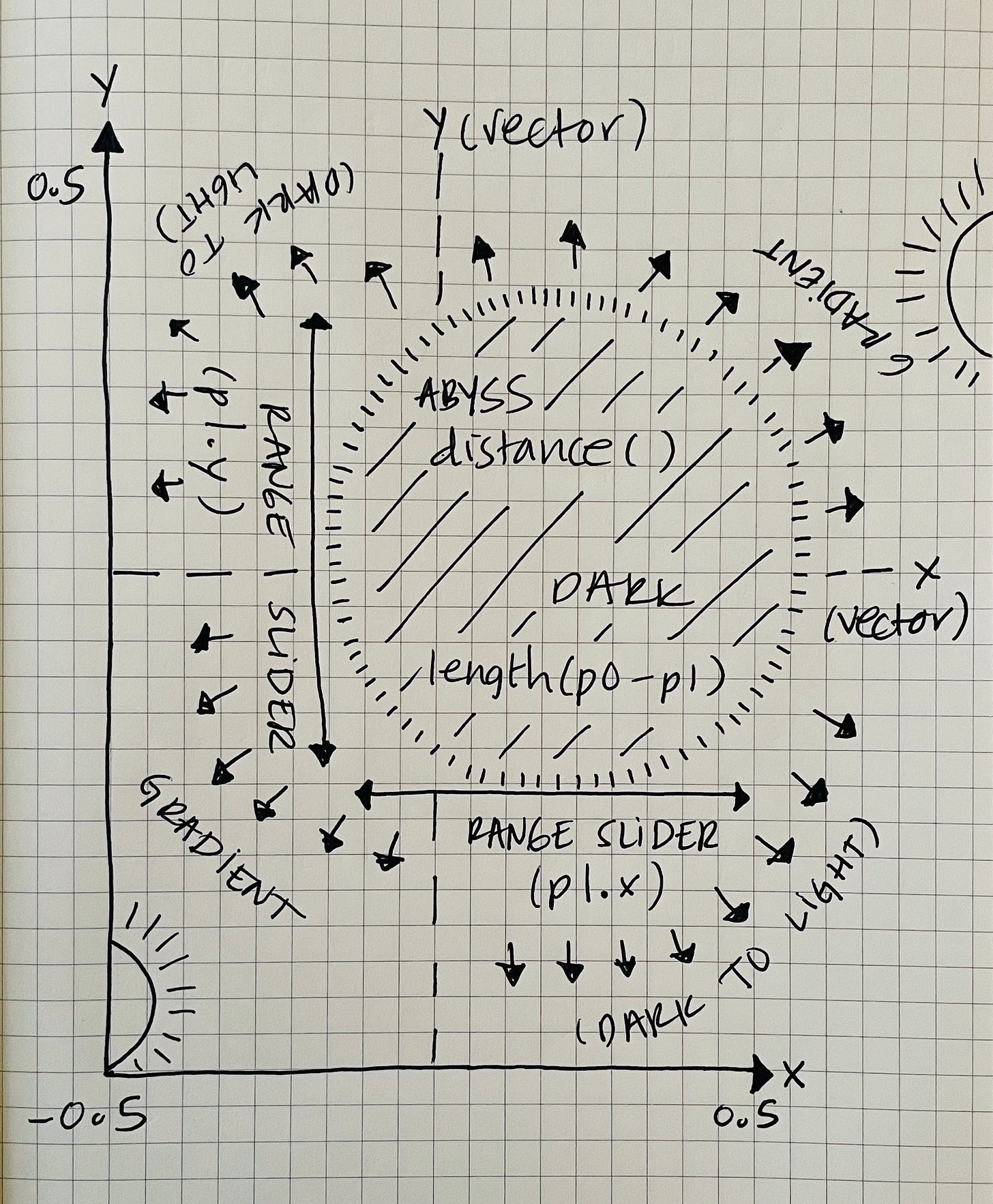
On the other hand, if we use a two-dimensional vector as p0, our imaginary abyss would no longer be flat but round, considering both coordinates in the space. It’ll still be an abyss, but a circular one, like a black hole that gradually dissipates towards the light, forming a radial gradient between a dark and a light color on our screen. Our p1, in this case, would no longer be a floating-point value but also a two-dimensional vector, as in order to measure the distance between those two points, we need to have the same kind of vector. A vector vec2(0.25, 0.0) would then act as a range slider (x, y), pushing our circular abyss to the right half of the screen.
No matter if our points to measure, p0 and p1, are one-dimensional or two-dimensional vectors, think of an imaginary abyss portrayed as two mirrored linear gradients or a radial gradient emerging from the center of the first point (p0) vector if your coordinate space is centered. In addition to picturing a range slider (second point — p1) for moving such an abyss over the p0 coordinate vector. As long as I imagine such gradient(s) with a range slider whenever I use this function, I can make a clear picture of what that code will draw.
References: