Shaders in sketches — Smoothstep
Hola,
Welcome to my tiny newsletter. :)
If you're here, you're probably curious about pixel shaders as much as I am. My intention with it is to share my way of understanding GLSL code when I write shaders.
Shaders can be a rather complex and intimidating computer program to explore when one's new to it, but maybe it's all about perspective and how one can interpret the program pieces to make them work.
To begin with, I'll take you on a journey of a small series of short thoughts on how my brain works when it tries to explain to me some of the GLSL built-in functions. Perhaps my way of understanding can help you too.
On my blog, I published the first short post from this 'Shaders in sketches' series about step(). Now, it's time to talk about another GLSL function.
I suggest you read the post mentioned above if you haven't yet, as I'm going to assume you know some details of how a pixel shader works, to avoid being as repetitive.
Smoothstep function
Let's travel through the smoothstep() function, which performs a Hermite interpolation between two values:
smoothstep(edge0, edge1, x) The links in the references below give us a description of this GLSL function:
smoothstep performs smooth Hermite interpolation between 0 and 1 when edge0 < x < edge1.
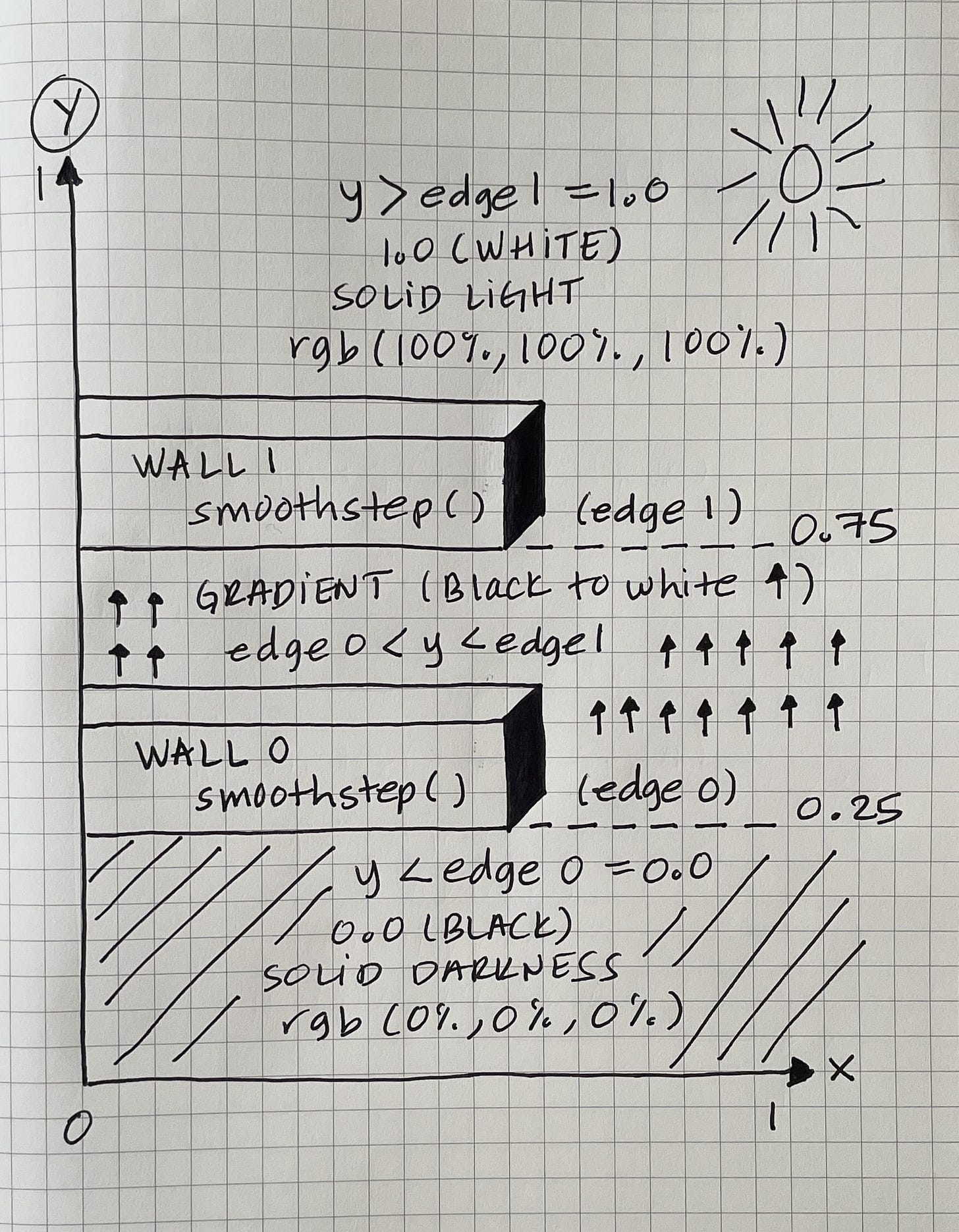
But what does that mean? My aha moment arrived, once I visualized the function as two tall walls separating two sides with solid colors, and a middle ground between walls having a gradient luminosity going from dark (leaking from wall 0) to light (leaking from wall 1).
The two colors are black and white. Black when getting 0, and white when getting 1.
In this exemplification, if smoothstep() has a lower edge of 0.25 and an upper edge of 0.75, we can assign a value of 0.0 to the edge that is closer to that floating-point number, in this case, is the lower edge (edge 0), and assign a value of 1.0 to the edge closer to this, being the upper edge (edge 1).
Once we've defined which edge has either a value of 0.0 or 1.0, we can assign such value to all three values from the RGB color model as vec3(0.0, 0.0, 0.0) = vec3(0.0) representing the color black, and vec3(1.0, 1.0, 1.0) = vec3(1.0) representing the color white. We can think of the edge's values of 0.25 and 0.75 as two points in a coordinate space from where we construct imaginary walls to place those solid colors that won't pass these walls.
And the in-between happening from the coordinate space of 0.25 - 0.75 results in what is called a Hermite interpolation which in my mind is the moment that both walls let some of their solid colors leak a bit, forming a gradient color going in a direction starting from the lower edge up to the upper edge, equivalent to going from down to up in our screen.
To make even more sense of this Hermite interpolation, we can also think that if we choose an equal lower and upper edge of 0.4, it would be nonexistent because we wouldn't have a gradient at all, imagining our two walls cemented from the same origin.
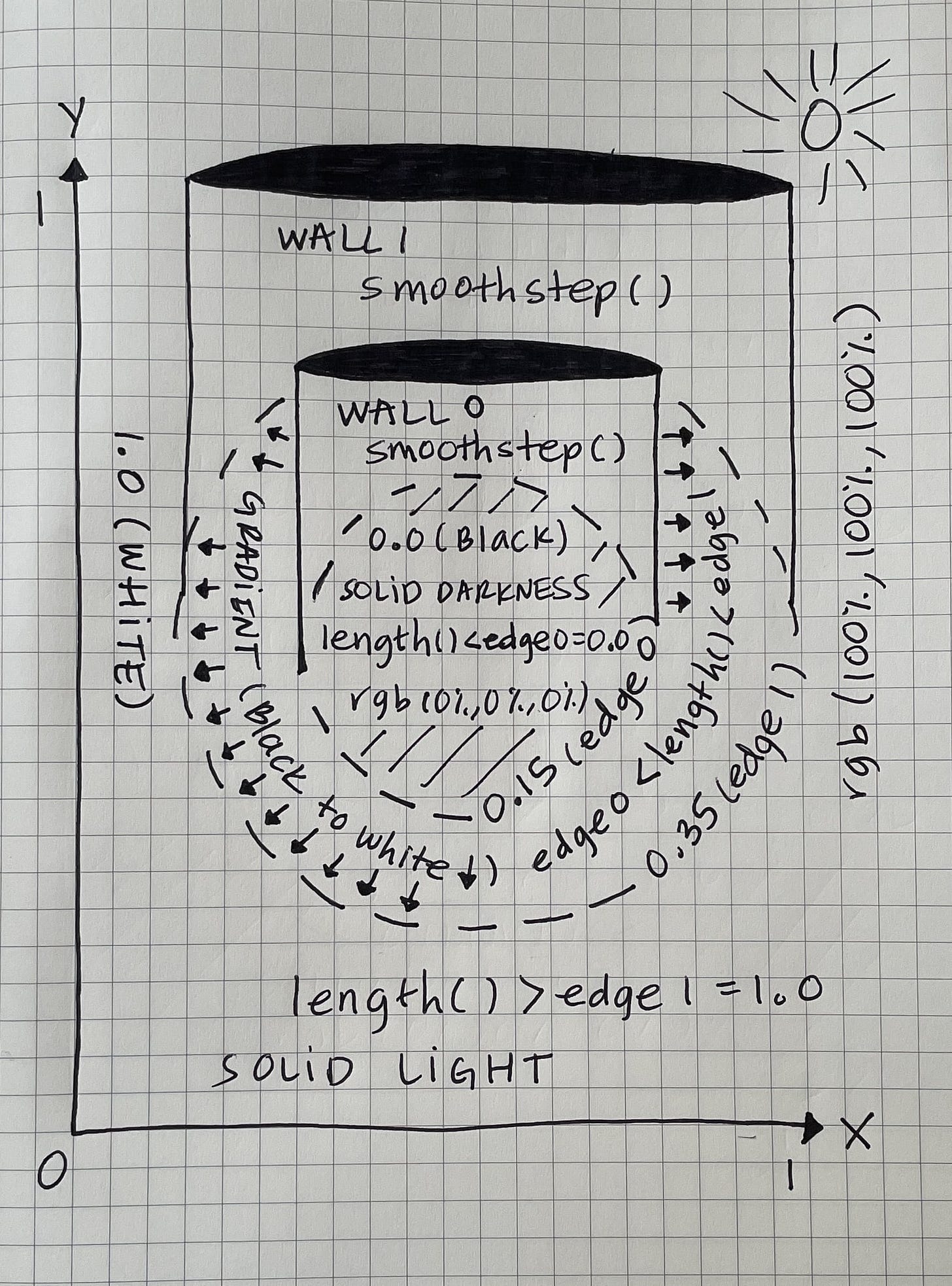
No matter if x is a linear coordinate or a distance between two or more points in a plane, build two imaginary walls splitting two colors to form a gradient in between. As long as I visualize such walls growing from two different edges whenever I use this function, I can make a clear picture of what that code will draw.
References: